Applications of derivatives: rate of change of bodies, increasing/decreasing functions, tangents and normal, use of derivatives in approximation, maxima and minima (first derivative test motivated geometrically and second derivative test is given as a provable tool)
To solve practical problems such as engineering optimization, the greatest challenge is often to convert the word problem into a mathematical optimization problem—by setting up the function that is to be maximized or minimized. Similarly, we can also find the rate of change of a body using differentiation.
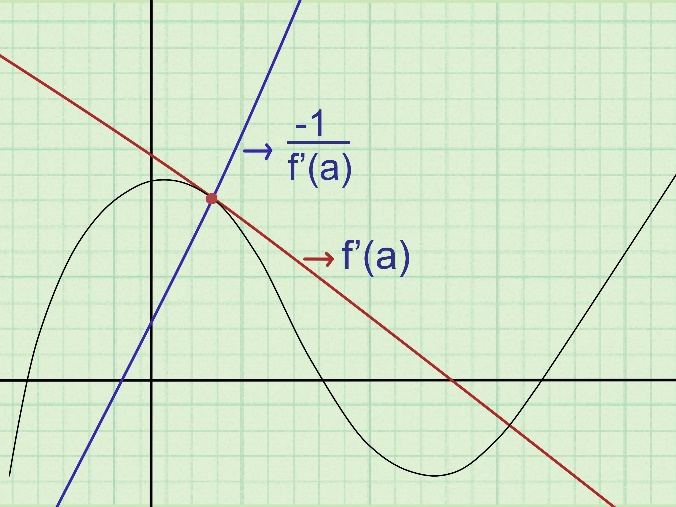
Recall that dy/dx is positive if y increases as x increases and is negative if y decreases as x increases.Also, the slope of the tangent of a curve f(x) can be found out by deriving the function of the curve at the given point. Because the normal line is perpendicular to the curve f(x) at a given point, the gradient of the normal is -1/f’(x).
Example: A ship can reach its top speed in 5 minutes.During that time its distance from the start can be calculated using the formula D = t + 50t2 where t is the time in seconds and D is measured in metres. How fast is it accelerating?
Speed, v m/s, is the rate of change of distance with respect to time.
v = 1 + (100 5) = 501 m/sec.
Acceleration, a m/s2, is the rate of change of speed with respect to time or second derivative of distance with respect to time.
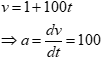
Now consider the graph below:
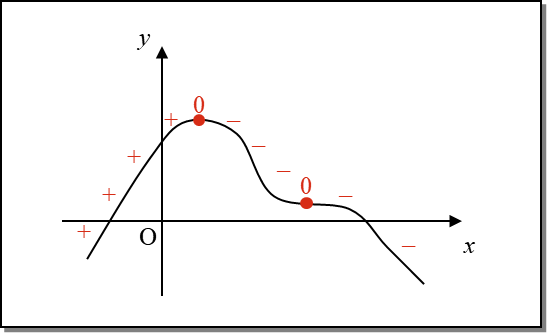
The signs indicate where the gradient of the curve is =, – or 0. In each case:
A function is strictly increasing in a region where f´(x) > 0. A function is strictly increasing in a region where f´(x) < 0. A function is stationary where f´(x) = 0
Example: f(x) = 2x3 – 3x2 – 12x + 1.
Identify where the function is (i) increasing (ii) decreasing (iii) stationery
Solution: f’(x) = 6x2 – 6x – 12
A sketch of the derivative shows us that
f´(x) < 0 for 0 <x< 2 … f(x) decreasing
f´(x) > 0 for x< 0 or x> 2 … f(x) increasing
f´(x) = 0 for x = 0 or x = 2 … f(x) stationary

When a function is defined on a closed interval, a ≤ x ≤ b, then it must have a maximum and a minimum value in that interval.
These values can be found either at
• a stationary point [where f´(x) = 0]
• an end-point of the closed interval. [f(a) and f(b)]
All you need do is find these values and pick out the greatest and least values.
Example: A manufacturer is making a can for holding 250 ml of juice.The cost of the can is dependent on its radius, x cm.For practical reasons, the radius must be between 2.5 cm and 4.5 cm.The cost can be calculated from the formula
C = x3 –5x2 + 3x + 15, 2.5 ≤ x ≤ 4.5.
Calculate the maximum and minimum values of the cost function.
Solution
which equals zero at stationary points.
3x2 – 10x + 3 = 0
- (3x– 1)(x – 3) = 0
- x = 1/3 or x = 3
- Working to 1 d.p.
- f(1/3) = 15.5
- f(3) = 6
- f(2.5) = 6.9
- f(4·5) = 18.4
- By inspection fmax = 18.4 (when x = 4.5) and fmin = 6 (when x = 3).

Let f : D → R, D ⊂R, be a given function and let y = f (x). Let ∆x denote a small increment in x. Recall that the increment in y is corresponding to the increase in x, denoted by ∆y, is given by ∆y = f (x + ∆x) – f (x). We define the following:
- The differential of x, denoted by dx, is defined by dx = ∆x.
- The differential of y, denoted by dy, is defined by dy = f′( x) dx
In case dx = ∆x is relatively small when compared with x, and for y, we denote dy ≈ ∆y.
Example: Use differential to approximate $\sqrt{36.5}$
Solution:
Take $y= \sqrt{x}$, let x = 36 and ?x=0.5
Therefore, $\Delta y$ = $\sqrt{x+\Delta x}-\sqrt{x}=\sqrt{36.5}-\sqrt{36}=\sqrt{36.5}-6$
Hence, $\sqrt{36.5}=6+\Delta y$
Since dy is approximate = $\Delta y$, it is given by:
$dy=(\frac{dy}{dx})\Delta x=\frac{1}{2\sqrt{x}}(0.5)=\frac{1}{2\sqrt{36}}(0.5)=\frac{1}{24}=0.04$, since $y= \sqrt{x}$
Therefore, the approx. value of $\sqrt{36.5}$ is 6 + 0.04=6.04