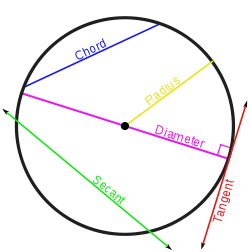
The geometric definition of a circle can be explained by a plane intersecting a circle.
A circle is created when the set of all points that are equidistant from a given point (the centre). Radius is a distance between the centre and any point on the circumference. The diameter cuts the circle in half. A line that connects one point on the edge of the circle with another point on the circle is called a chord. A tangent is a line that intersects the circle at exactly one point and not more while a secant intersects at 2 points. The circumference or perimeter of a circle is the distance around the circle.
Theorems
1. On a plane, a line is a tangent to a circle if is perpendicular to a radius of the circle at its endpoint on the circle.
2. Two circles with the same radius are congruent and two arcs are congruent if they have the same measure and they are arcs of the same circle (or congruent circles).
3. In a circle, two minor arcs are congruent when they have corresponding chords to be congruent as shown in the figure below.

For example, In the diagram, P ≡ Q, FG≡ JK , and mJK = 80°. Find mFG.
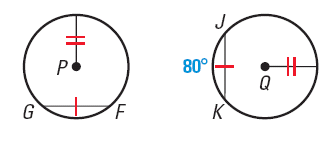
So, mFG= mJK= 80o.
4. If one chord is ꓕ bisector of another chord, then the first chord must be a diameter.
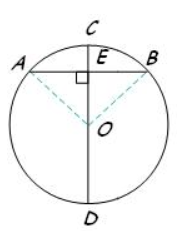
5. If the diameter is ꓕ to a chord, then the diameter must bisect the chord and its arc.
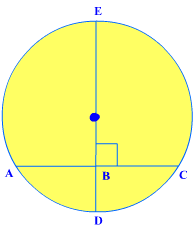
For example, Use the diagram of pointEto find the length of AC.
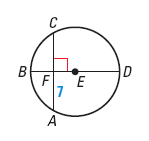
Diameter BD is perpendicular to AC. So, according to the Theorem, BD bisects AC, and CF = AF.
This means, AC = 2 AF = 2(7) = 14.
6. In the same circle, two chords are congruent if they are equidistant from the centre.
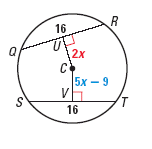
For example, In the diagram of C, QR = ST = 16. Find CU.
CU = CV
2x = 5x – 9
x = 3
So, CU = 2x = 2(3) = 6.
7. The angle of an inscribed angle is ½ of its intercepted arc. An inscribed angle has vertex on a circle and whose sides contain chords of the circle.
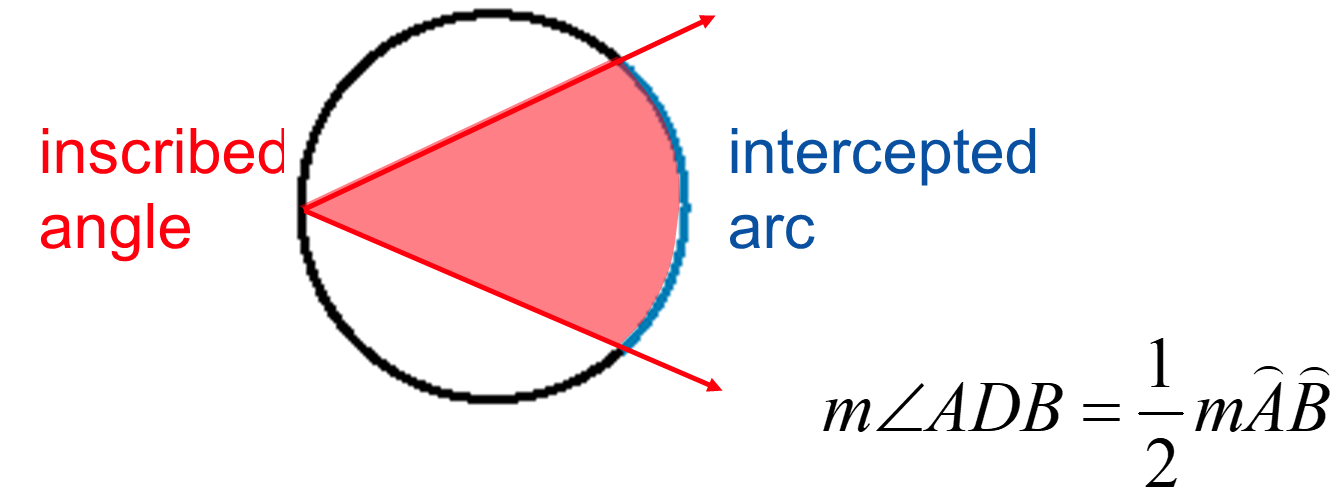
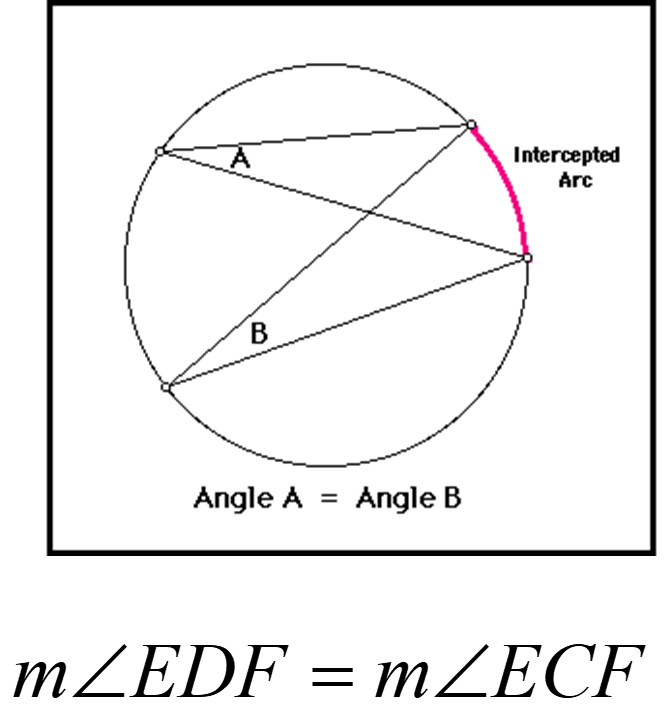
8. If two inscribed angles in a circle intercept the same arc, the angles are congruent.
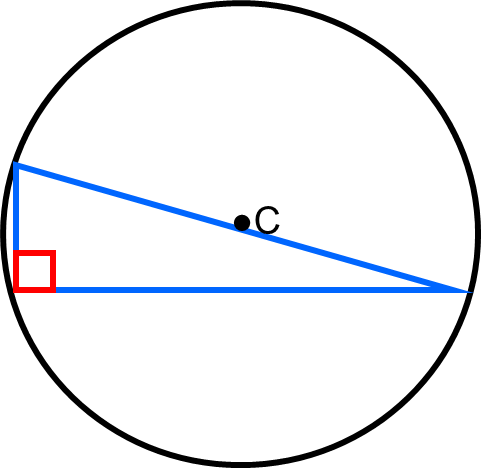
9. A right triangle is inscribed in a circle if the hypotenuse is a diameter of the circle.
10. If a tangent and a chord intersect at a point on a circle, the measure of every angle formed is half the measure of its intercepted arc.


