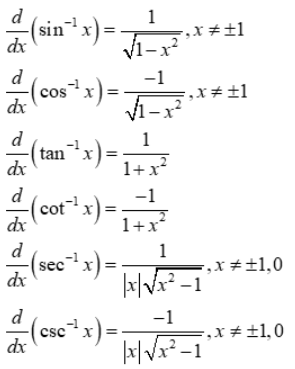Continuity and differentiability, derivative of composite functions, chain rule, derivatives of inverse trigonometric functions, derivative of implicit functions and differentiability
The derivative does not exist (the function is not differentiable) at any point where the function is not continuous. Therefore, if the function is not continuous it’s also not differentiable.
But even if the function is continuous at a point, it still might not be differentiable there. These conditions need to be fulfilled for the function to be differentiable at a given point:
1. The function must be continuous at the given point.
2. The graph is smooth with no sharp bend at the given point
3. The tangent line is oblique (slanted) or horizontal, and not vertical.
Hence, a function f is continuous at the point x = a if the following are true:
- f(a) is defined
- $\lim _{x\to a}f(x)$ exists
- $\lim _{x\to a}f(x)=f(a)$

If f and g are continuous at x = a, then $f\pm g,\frac{f}{g} such that (g(a)\ne 0)$ are continuous at x = a
Recall that a polynomial function y = P(x) is continuous at every point x and a rational function ![]() is continuous at every point x in its set domain.
is continuous at every point x in its set domain.
Example: At which value(s) of x is the given function discontinuous?
$f(x)=x+2$
This function is continuous everywhere:
$\lim _{x\to a}f(x)=f(a)$
$\lim _{x\to a}(x+2)=a+2$
$g(x)= \frac{x^{2}-9}{x+3}$
This function is continuous everywhere except at a point x = -3
g(-3) is undefined
The composite function h = g ◦ f defined by h(x, y) = g(f(x, y)) is also a continuous function
- What is $\frac{d}{dx}(f(u))$ where $u$ is a function of $x$?
- Chain rule: $\frac{df}{dx}=\frac{df}{du}\cdot \frac{du}{dx}$
- Example: If $f(x)= \sqrt{1+x^{2}}$ then taking $u=1+x^{2}$ and $f(u)= \sqrt{u}$ $\frac{df}{dx}=\frac{df}{du}\cdot \frac{du}{dx}=\frac{1}{2\sqrt{u}}\cdot 2x=\frac{x}{\sqrt{1+x^{2}}}$
Observe that F is a composite function. In fact, if we let y = f(u) = $\sqrt{u}$ and let u = g(x) = x2 + 1, then we can write y = F(x)= f (g(x)): F = f∙g. It turns out that the derivative of the composite function f ◦ g is the product of the derivatives of f and g.
Implicit differentiation: Although we can not solve explicitly for y, we can assume that y is some function of x and use implicit differentiation to find the slope of the curve at a given point y= f(x)
If y is a function of x then its derivative is dy/dx. y2 is a function of y, which in turn is a function of x and here we can use chain rule: $\frac{d}{dx}\lbrack y^{2}\rbrack =2y\frac{dy}{dx}$
- For performing implicit differentiation, differentiate both sides of the equation with respect to x, treating y as a function of x. This requires the chain rule.
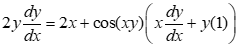
- Collect terms containing $\frac{dy}{dx}$ on one side of the equation
- Factor $\frac{dy}{dx}$
- Solve for $\frac{dy}{dx}$
We can use the chain rule for finding derivatives of inverse trigonometric functions:
Example: $f(x)=\sin ^{-1}x$ find f'(x)
Solution: Let y = $\sin ^{-1}x$ then we know that x = sin y
When we differentiate both sides we obtain
$1=\cos y \frac{dy}{dx}=\frac{1}{\cos (\sin ^{-1}x)}$
This property is defined only for cos y ? 0, hence $\sin ^{-1}x\ne -\frac{\pi }{2},\frac{\pi }{2}$ and $x \ne -1,1$
$\cos ^{2}y=1-(\sin y)^{2}=1-(\sin (\sin ^{-1}x))^{2}=1-x^{2}$
Thus for $x ∈ (-1,1)$,
$\frac{dy}{dx}=\frac{1}{\cos y}=\frac{1}{\sqrt{1-x^{2}}}$
Derivatives of Inverse Trigonometric Functions