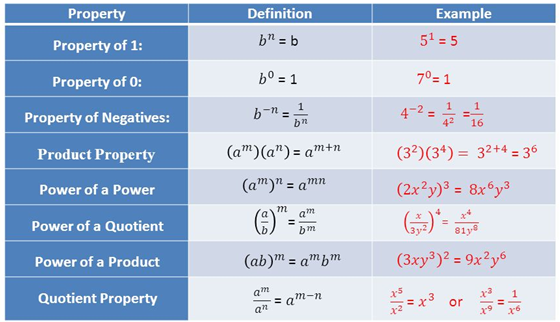
The function defined by f(x) = bx; (b>0), b≠1) is called an exponential function with base b and exponent x.Here, the domain of f can be explained as a set of all real numbers. Let m and n be positive numbers and let a and b be real numbers. Then,
The exponential function y = bx (b> 0, b ≠ 1) is associated with the following properties:
-
- The domain is (–∞, ∞).
- Range is (0, ∞).
- The graph passes through the point (0, 1)
- Continuous on (–∞, ∞).
- Increasing function on all real numbers (–∞, ∞); b>1 and a decreasing function on (–∞, ∞); b< 1, such that b ≠ 1.
Exponential functions to the base e play a prominent role in theoretical and applied problems such as growth and ready of a natural phenomenon. Here e is an irrational number whose value is 2.7182818…. It can be shown that
$e=\lim _{m\to \infty }(1+\frac{1}{m})^{m}$
You can write an exponential equation as a logarithmic equation and vice versa in the following format.
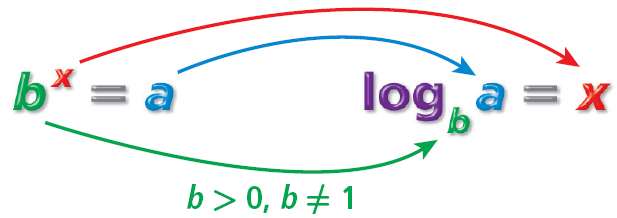
The function defined by f(x) = logbx; (b>0, b≠1) is called the logarithmic function with base b. The domain of f is this case is a set of all positive numbers and not real numbers. The following properties of logarithmic functions show M and N as positive real numbers, b ≠ 1, such that p and x are real numbers.
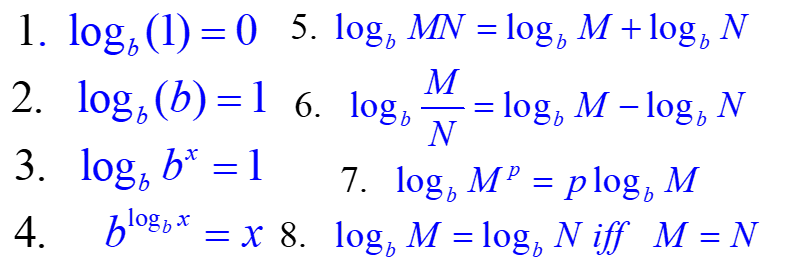
The function logba= x is read as “the log base b of a is x.” Notice that the log is the exponent.A logarithm containing base 10 is defined as a common logarithm. A logarithm containing base e is defined as a natural logarithm. When no base is mentioned for a logarithmic function, the base is assumed to be 10. For example, log 5 = log105.
![]()
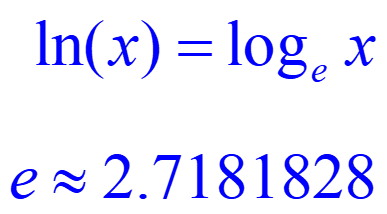
Properties relating ex and ln x:
- elnx = x (x> 0)
- ln ex = x (x = real number)
Logarithms are the inverses of exponents, the inverse of an exponential function, such as y = 2x, is a logarithmic function, such as y = log2x.The domain of y = 2x is all real numbers (R), and the range is {y|y> 0}. The domain of y = log2x is {x|x> 0}, and the range is all real numbers (R).
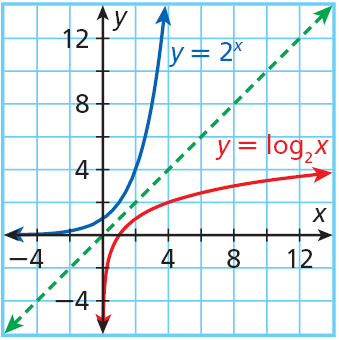
The logarithmic function y = logbx (b > 0, b ≠ 1) is true for the following properties:
-
- Domain is (0, ∞).
- The range is (–∞, ∞).
- The graph passes through the point (1, 0).
- Continuous on (0, ∞).
- Increasing fucntion on the range (0, ∞); b > 1 and a decreasing function on (0, ∞); b < 1, such that b ≠ 1.
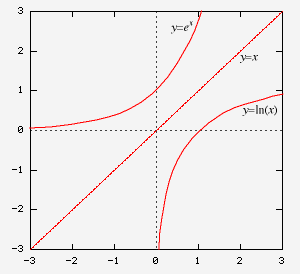
Example: Sketch the graph of y = ln x and show its relationship with y = x.
Solution: The required graph is the mirror image of the graph of y = ex with respect to the line y = x: