An invertible matrix A is called a row equivalent to an identity matrix, and we can this matrix by understanding the row reduction of A to I.
A n x n matrix A is invertible if and only if A is row equivalent to In, and in this case, any sequence of elementary row operations that reduces A to In also transforms In into A-1.
Proof: Suppose that A is an invertible matrix.Then, since the equation Ax =b has a solution for each b, A has a pivot position in every row.Because A is square, the n pivot positions must be on the diagonal, which implies that the reduced echelon form of A is In. A˜In.Then, since each step of the row reduction of A corresponds to left-multiplication by an elementary matrix, there exist elementary matrices E1, …, Ep such that A~E1A~E2(E1A)~…~Ep(Ep-1…E1A)=In
Therefore, Ep…E1A = In. Since the product Ep…E1 of invertible matrices is invertible, the equation leads to (Ep…E1)-1 (Ep…E1)A = (Ep…E1)-1In
A = (Ep…E1)-1
When a matrix A is invertible, the equation A-1 Ax = x can be applied as statement for linear transformations. See the following figure:
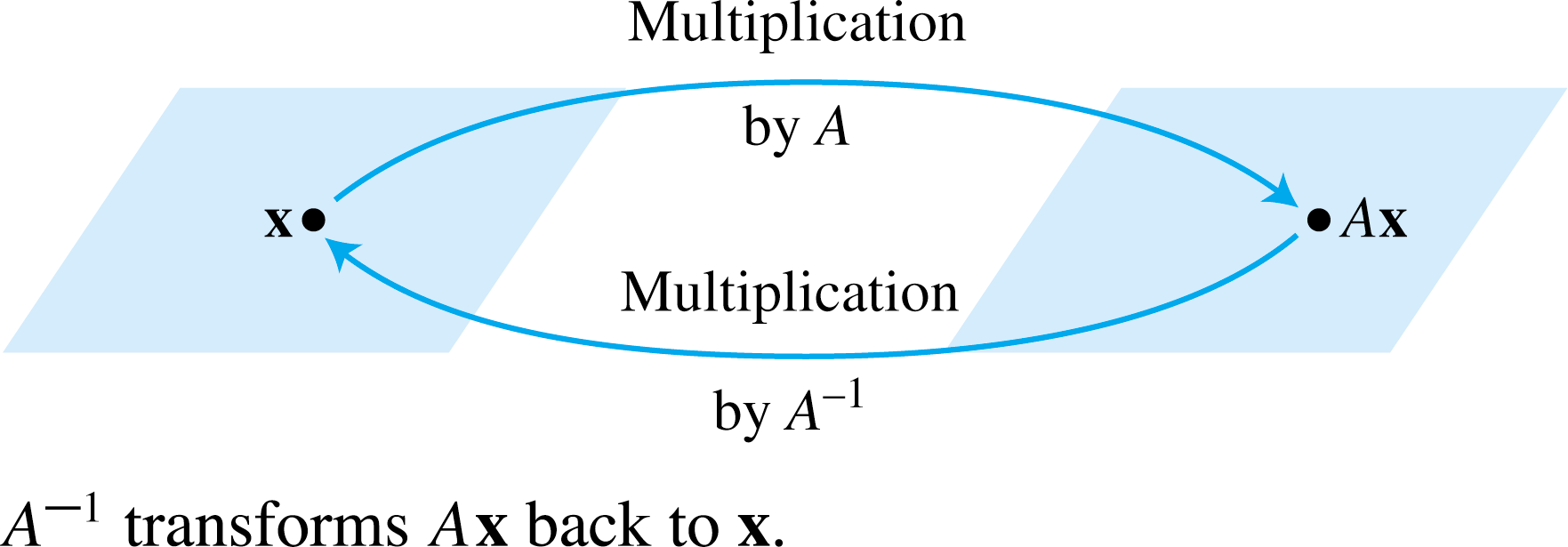
The inverse of a matrix is defined by AB = I = BA if and only if A is the inverse of B.
We then write: AA-1 = A-1A = 1 = BB-1= B-1B. Consider the general matrix expression below:
AX = B
A-1AX = A-1B
A-1AX = A-1B
1 X = A-1B
X = A-1B
If A and B are invertibile matrices having same order, then (AB)-1 = B-1 A-1.
From the definition of inverse matrix, we know that:
(AB) (AB)–1 =1
A–1 (AB) (AB)–1 =A–1I (Pre multiplying both sides by A–1)
(A–1A) B (AB)–1 =A–1 (Since A–1 I = A–1)
IB (AB)–1 =A–1 or B (AB)–1 =A–1
B–1 B (AB)–1 =B–1 A–1
I (AB)–1 =B–1 A–1
Thus, (AB)–1 =B–1 A–1
Uniqueness of inverse: If an inverse of a square matrix exists, it is unique.
Proof: Let A = [aij] to be a square matrix havingan order of m. Let B and C be two possible inverses of A. If the inverse is unique, then B = C
Therefore, AB = BA = I and AC = CA = I since both B and C are inverse of A.
Hence,
B = BI = B(AC) =(BA)C = IC = C