Statistics – Measures of dispersion: Variance
Variance(σ2 ) is a measure of how data points differ from the mean. It is defined as the average of the squared deviations for data set values:
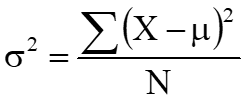
First, the formula says to subtract the mean from each of the scores. The difference of these quantities is called a deviate or a deviation score which explains how far a given score is from the typical, or average, score. Therefore, deviate is essentially a measure of dispersion for a given data set. In order to conceptualize the spread of a distribution as the extent to which the values in the distribution are different from each other as well as the mean, we need a reasonable measure of spread that can either be the average deviation, or difference, of the values from the mean as shown below.

Although it may seem unreasonable, the expression above equals 0. This happens because the -ive deviations about the mean always cancel out the +ive deviations about the mean. Therefore, we use the absolute sign to remove the possibility of numbers canceling each other, which is the same mathematically as taking the absolute value, which is known as the mean deviations. Likewise, the average value from the squared deviations about the mean is called the variance. Note that, the total average squared deviation from the mean value of X is smaller than the average squared deviation from any other value of X.
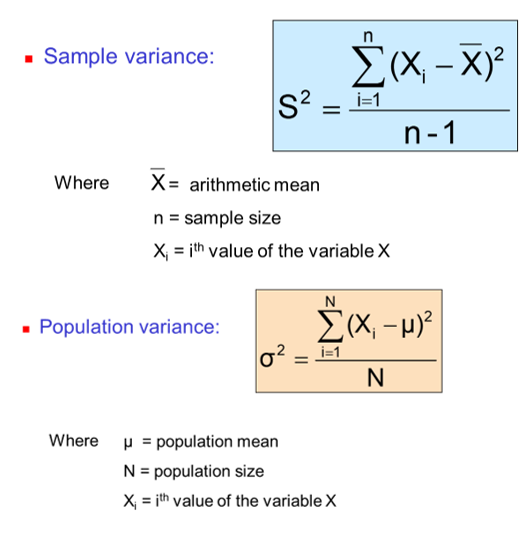
From the formulae above, we can conclude that, the larger the variance is, the more the data points deviate, on average, away from the mean. Likewise, the smaller the variance is, the less the data points deviate, on average, from the mean.
Consider the data set; 3, 5 7, 10, 10
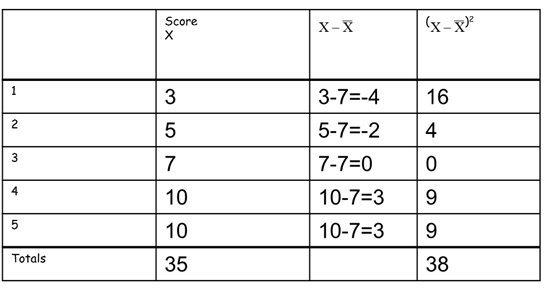
$s^{2}=\frac{38}{4}=9.5$
The variance is a frequently used measure of dispersion used in statistical theory. However, it has a drawback when researchers want to describe the dispersion of data in a practical format. The unit of variance is squared of the units of original data as well as the mean deviation and average values. This means that it is difficult to bring any intuitive or practical sense of the variance value. This drawback can be eliminated by finding the (positive) square root of the variance (which takes us back to the original units).The measure of the square root of the variance is known as the standard deviation.