A family of lines is a set of lines having one or two factors in common with each other. Straight lines can belong to two types of families: one where the slope is the same and one where the y-intercept is the same.
Consider the two straight lines
- a1x+b1y+c1=0
- a2x+b2y+c2=0
For any nonzero constant k, the equation of the form
- a1x+b1y+c1+k(a2x+b2y+c2)=0
being linear in x and y is an equation of a straight line.
If (x1,y1) is the point of intersection of line 1 and 2, then it must satisfy both equations 1 and 2:
- a1x1+b1y1+c1=0
- a1x1+b2y1+c2=0
Next, we check whether the point (x1,y1) lies on 3 or not. For this, we replace x by x1 and y by y1 in equation 3, and we have
- a1x1+b1y1+c1+k(a2x1+b2y1+c2)=0
Using equation 4 and 5 in equation 6, we get the following result:
0+k(0)=0
This shows that equation 6 is true for all k and for x=x1,y=y1. Thus, the point (x1,y1) lies on 6 for all k. Equation 6 represents the equation of the line through the point of intersection of lines 1 and 2. Since k is any real number, equation 6 shows that there will be an infinite number of lines through the point of intersection of lines 1 and 3.
We must have the particular value of k find the equation of a line, and this particular value of kcan be found with the help of some given conditions.
Example 1: Find the equation of a line through the point (1,3) and the point of intersection of lines 2x−3y+4=0 and 4x+y−1=0.
The equation of a straight line through the point of intersection of lines 2x−3y+4=0 and 4x+y−1=0 is given as
2x−3y+4+k(4x+y−1)=0
Since the required line passes through the point (1,3), this point must satisfy the equation, i.e.
2(1)−3(3)+4+k(4(1)+3−1)=0−3+6k=0
k=12
Putting this value of k in the required equation of a straight line, we have
2x−3y+4+12(4x+y−1)=0
4x−6y+8+4x+y−1=0
Answer: 8x−5y+7=0
Example 2. Write the equation of the family of lines satisfying the following conditions:
a) parallel to the x-axis
b) through the point (0, -1)
c) perpendicular to 2x+7y−9=0
d) parallel to x+4y−12=0
a) All lines parallel to the x-axis have a slope of zero; the y-intercept can be anything. So the family of lines is y=0x+b or just y=b.

c) First, we need to find the slope of the given line. Rewriting 2x+7y−9=0 in slope-intercept form, we get y=−27x+97. The slope of the line is −27, so we’re looking for the family of lines with slope 72.
The family of lines is y=72x+b.
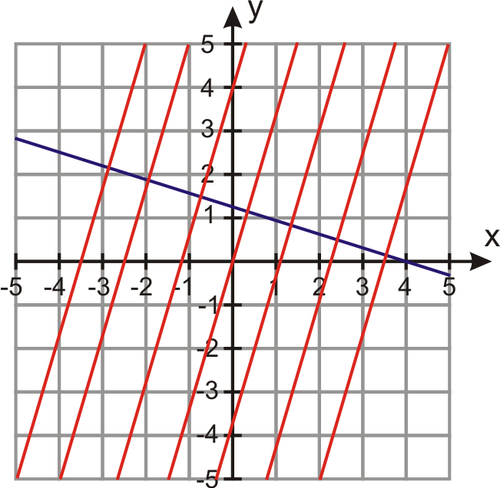
d) Rewrite x+4y−12=0 in slope-intercept form: y=−14x+3. The slope is −14, so that’s also the slope of the family of lines we are looking for.
The family of lines is y=−14x+b.
