Modulus function or absolute value function is said to be the one that consists of algebraic expressions that are enclosed within various absolute value symbols. Now, you must be aware of the fact that the absolute value of a number is determined by its distance from zero on the number line.
Domain and range of Absolute Value Function (Modulus function)
Consider this parent function (absolute value function) it would be noted down as: $f(x)=|x|$ and defined as under:
$f(x)=x$ if $>0$;
$f(x)=0$ if $=0$;
$f(x)=-x$ if $<0$
In order to graph an absolute value function, you would be required to look for certain values for x and make up some ordered pairs. For instance, consider the below-mentioned values for x and y.
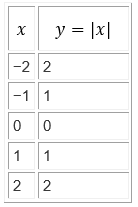
Now, plot these points on the coordinate plane and connect those.
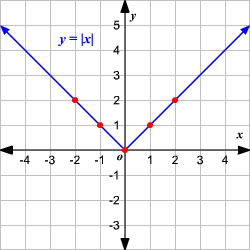
Absolute Value Graphs
The observer can make out several points about the graph. These graphs would mostly turn out to be V-shaped. The addition or subtraction of values would determine the transformation of the absolute value graph you may be dealing with.
For all functions, the x values would comprise the domain set and y values would comprise the range set. The domain should always move from negative to positive infinity $-\infty +\infty $ which is likely to go on endlessly. Ranges for these are supposed to be specific with the vertex as its limit.
Several observations on the graph:
- The vertex of such graph would be determined at (0,0).
- The graph gets divided into congruent halves with a line (axis of symmetry) where $x=0$.
- The domain is said to be consisting of all real numbers.
- The range is supposed to be a set of real numbers that are either equal to or greater than 0. i.e. $y\ge 0$.
- The x and y intercepts are both zero.
Changes in the absolute value graph
Vertical shift
The absolute value function $f(x)=|x|$ can be translated vertically by using the function $g(x)=f(x)+k.$ When $k>0$, the graph gets translated up by $k$ units. And $k<0$, the graph gets translated down by $k$ units.
Horizontal Shift
The function $f(x)=|x|$ can be translated using the function $g(x)=f(x-h).$ When $h>0$, the graph of $f(x)$ gets translated to the right by $h$ units. And when $h<0,$ the graph gets translated to the left by $h$ units.