If the sequence is geometric, then without really adding all the actual terms, there are methods for finding the sum of 1st n terms, which are denoted by Sₙ.
With the use of the formula, you can find the sum of the first Sₙ terms of the geometric sequence
Sn = a₁(1−rⁿ) / 1−r, r≠1
Where,
n = number of terms,
a₁ = first term and,
r = common ratio.
Now, the sum of first n terms of the geometric sequence is known as the geometric series.
Now, comes G.P.’s sum to infinity =
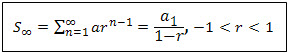
Where,
r = common ratio
a1 = first term
S∞ = G.P.’s sum with infinitely many terms
Sn = G.P.’s sum with ‘n’ terms
n = number of terms
Example 1: Find the sum of the 1st 7 terms of a geometric series, if
a1 = 1 & r = 2.
S8 = 1 (1−2⁷) / 1−2
= 1- 128 / -1
= 127
S₇ = 1(1−2⁷) / 1−2= 127
Example 2: Find S₈ of a geometric sequence 36,18,9,⋯.
First, find r.
r = r2 / r1 = 18 / 36 = 1/2
Now, we have to find out the sum:
S₈ = 36. (1−(1/2)⁸) / 1−1 /2 = 2295/32
To obtain the sum which is having an “infinite geometric series”, the “r” which is the common ratio should be lying between -1 & +1. Accordingly, as the value of n increases, rⁿ get closer to the value zero. For finding the sum of the infinite geometric series, which contains the ratios, having an absolute value which is less than 1, so, use this formula:
S = a1 / 1−r
where,
a₁ = first term &
r = common ratio.
Example 3: Finding the number of terms in the G.P
8, 16, 32, ……..512
a₁ = 8; a₂ = 16 ; a₃ = 32; aₙ = 512
r = a₂ / a₁ = 2
⇒ 512 = a₁. rⁿ⁻¹
⇒ 512 = 8. (2)ⁿ⁻¹ (substituting the values)
⇒ 512 / 8 = (2)ⁿ⁻¹ (on dividing 512 by 8)
⇒ 64 = (2)ⁿ⁻¹ (change 64 to its exponential form)
⇒ 2⁶ = (2)ⁿ⁻¹ (Now, equate the indices as they both contains the same base)
⇒ 6 = n – 1
⇒ n= 7
Example 4: To find the sum of geometric series -3, ⅓, -1/27……… -1/19683
Here:
a₁ = -3; a₂ = 1/3 ; a₃ = -1/27; aₙ = -1/19683
r = a₂ / a₁ = -1/9
⇒ -1/19683 = a₁. rⁿ⁻¹
⇒ -1/19683 = (-3). (-1/9)ⁿ⁻¹ (substituting values of a₁, aₙ, r, & aₙ = a₁.rⁿ⁻¹ to find n
⇒ -1/59049 = (-1/9)ⁿ⁻¹ on dividing both sides by (-3)
⇒ (-1/9)⁵ = (-1/9)ⁿ⁻¹ Change -1/59049 to its exponential form, whose base is ‘r’
⇒ 5 = n -1 Now, equate the indices as both are having the same base
n = 6
Now,
S₆ = Now, substitute the values of a₁, n, r to Sₙ {Sₙ = a₁ (1-rⁿ) / 1-r}
S₆ = -3. (1- (-1/9)⁶) / 1-(-1/9)
S₆ = -3 (1- (-1/531441) / 10/9
S₆ = -3 (531145 / 531144) / 10/9 Divide -3 (531145 / 531144) by 10/9
S₆ = 106229/3944