While you may have known about various types of functions, their domain and range, it is equally worthy to know about signum function.
Signum Function
The signum function is defined as $f(x)=\frac{x}{|x|}$ where;
$f(x)=-1$, when $x<0$ $f(x)=0$, when $x=0$ and; $f(x)=1$, when $x>0$.
It could also be said that the signum function returns -1, 1 or 0 in cases where the value of x is negative, positive or zero respectively.
The graph of a signum function would appear like the one illustrated below:
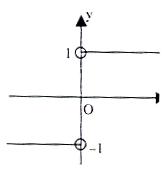
Here, f(x) is known to be continuous for all values of x except the one where x = 0, which creates a break in the curve. The domain of the function f(x) is x ∈ R and Range is set {-1, 0, 1}.
Diving further…
Any considerable real number can be expressed as the product of its absolute value and the sign function. That is:
$x=sgn(x).|x|$
With this equation, it could be made out that whenever x ≠ 0, the function would be
$sgn(x)=\frac{x}{|x|} $
The signum function is known to be the derivative of its absolute value function (till the indeterminacy of zero). Make a note of the fact that the resultant power of x is 0 which is even similar to any of its ordinary derivatives. These numbers tend to get canceled and all we are left with is the sign x.
$\frac{d|x|}{dx}=sgn(x)$ for $x\ne 0 $
The signum function could be differentiable through derivative 0 at any place except at 0. At 0, it isn’t differentiable in an ordinary sense. However, under the generalized notion of differentiation as per the distribution theory, the derivative of the same signum function is regarded to be two times of the Dirac delta function.
$\frac{d sgn(x)}{dx}=2\delta (x)$
Signum function for complex arguments
For any considerable complex number z, the signum function would be defined as:
$sgn(z)={0 when z=0, \frac{z}{\vert z\vert } when z\ne 0}$
In other words, when z is not equalizing zero, sgn(z) would be a projection of z onto the unit circle:
${z ∈ C|\vert z\vert =1}$
It is very clear that for real arguments, the complex signum functions tend to reduce to real signum function. For every, you will have:
zsgnz– = |z|
where z– is known to be the complex conjugate of z.
The above-mentioned details would help in understanding signum function and its domain and functions well. You may get onto its application in different conditions based on the properties explained above. This is something important while you seek to implement best practices with functions and relations.