Rolle’s and Lagrange’s Mean Value Theorems (without proof) and their geometric interpretation
Like many basic results in the calculus, Rolle’s theorem also seems obvious yet important for practical applications. It just says that between any two points where the graph of the differentiable function f (x) cuts the horizontal line there must be a point where f ‘(x) = 0.If you connect points f (a) to f (b) in a smooth curve,there will be at least one place where f ’(c) = 0.

If two points at the same height are connected by a continuous, differentiable function, then there has to be at least one place between those two points where the derivative, or slope, is 0.
Example: f(x) = x4 – 2x2 on [-2, 2]
Solution: Here we notice that: f(-2) = 8 = f(2)
Therefore, f is a continuous and a differentiable equation where Rolle’s Theorem applies:
f’(x) = 4x3 – 4x = 4x(x2 – 1) = 0 then x = -1, x = 0 and x = 1.
Example: consider point [-1, 1] where f(x) applies:
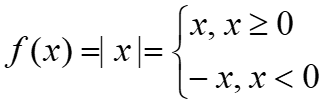
This function is continuous on [-1, 1] but it is not differentiable at 0 and (-1, 1) since,
f(-1) = 1 = f(1), Rolle’s theorem does not apply.
Lagrange’s Mean Value Theorem is one of the most important theoretical tools in Calculus. It states that if f(x) is a defined function which is continuous on the interval [a,b] and differentiable on (a,b), then there is at least one point c in the interval (a,b) (that is a<c<b) such that
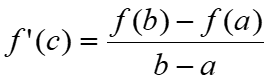
In other words, there exists a point in the interval (a,b) which has a horizontal tangent. In fact, MVT can be stated also in terms of slopes. Indeed, the number
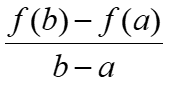
is the slope of the line passing through (a, f(a)) and (b, f(b)). We can also say that there exists a point such that the tangent line is parallel to the line passing through (a, f(a)) and (b, f(b)).
The figures show the points A(a, f(a)) and B(b, f(b)) on the graphs of two differentiable functions.
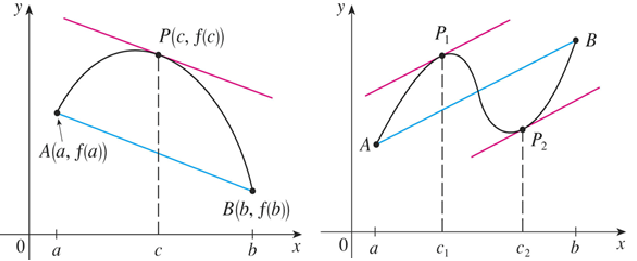
The slope of the secant line AB is:
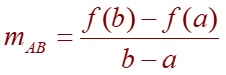
f ’(c) is the slope of the tangent line at (c, f(c)). So MVT states that there is at least one point P(c, f(c)) on the graph where the slope of the tangent line is the same as the slope of the secant line AB. So, MVT states that there is at least one point P(c, f(c)) on the graph where the slope of the tangent line is the same as the slope of the secant line AB.
Example:

Example: When an object is removed from a furnace and placed in an environment with a constant temperature of 90o F, its core temperature is 1500o F. Five hours later the core temperature is 400o F. Explain why there must exist a time in the interval when the temperature is decreasing at a rate of 220o F per hour.
Solution: Let g(t) represent the temperature of the object.Then g(0) = 1500, g(5) = 400
Avg temp = $\frac{g(5)-g(0)}{5-0}=\frac{400-1500}{5}=220$
By MVT, there exists a time 0 <to<5, such that g’(to) = –220o F