You may have already been introduced to finding averages. Well, arithmetic mean is just that.
Understanding Arithmetic Mean
In general language, average data and arithmetic mean are synonymous. It could also be referred to as the representative value for a group of data. Suppose that you have been given n number of elements and required to find the arithmetic mean for them all you will have to do is to sum up all the numbers and divide it with the total numbers.
If you’ve been looking for a definition, the arithmetic mean for a set of values could be defined as the ratio of the sum total of the values to the total number of values that are included in the set. Suppose that a data set consists of n numbers in a data set whose values had been given by the group of x values then, the arithmetic mean of these values could be recognized with the formula below:
$m=\frac{x_{1}+x_{2}+x_{3}+ \ldots +x_{n}}{n}$
A mean could be described as one of the simplest mathematical averages in order to find the average of a set of two or more numbers. There could be more than one ways to find the average for any set. However, the arithmetic mean is probably the most common one.
In simple terms, $Mean= \frac{Sum of all observations }{Total number of observations} $
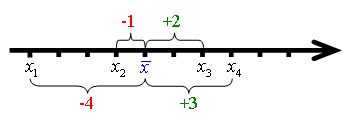
The arithmetic mean is often represented by $\bar{x}$. If such is the case then,
$\bar{x}=\frac{x_{1}+x_{2}+x_{3}+ \ldots +x_{n}}{n} = \frac{\sum_{i=1}^{n}{x_{i}}}{n}$
Here, the symbol ∑ stands for summation i.e. the sum total of these elements included.
Consider the below example for mean calculation:
The average salary earned by 20 employees in a company is 300. In the same company, the average salary of non-officers is 120. If the average salary of the entire organization is 150, find out the total number of non-officers in the company.
Solution: there could be two methods of solving this. Considering the conventional method, suppose the number of non-officers to be N. Since we know that the salaries of the officers and non-officers would give the total salary of the company, the equation can be created as: 20 × 300 + 120 × N = 150 (20 + N).
Solving it further, N = 100.
Along with this, you may require thinking logically that every officer is earning (300 – 150 = 150) i.e. Rs. 150 more than the average salary. The total extra money that all officers get will be 150 × 20 = 3000. Also, every non-officer gets (150 – 120) = Rs. 30 less than the average pay. The officers getting paid less will be 3000/30 = 100. Thus, there are 100 non-officers.