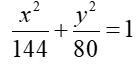The equation of an ellipse with its centre at the origin has one of two forms:
Horizontal Ellipse
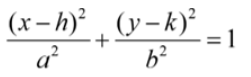
Foci:
![]()
![]()
Vertical Ellipse:
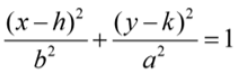
Foci:
![]()
For a horizontal Major Axis and C(0,0): major axis = 2a and minor axis = 2b

For a Horizontal Major Axis and C(h,k):
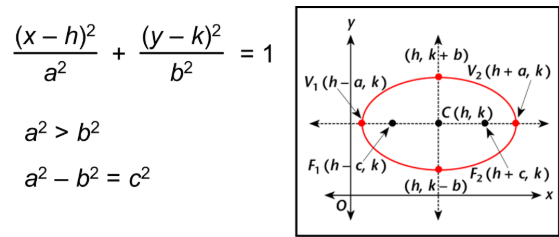
For a Vertical Major Axis and C(0,0), major axis = 2a and minor axis = 2b:

For a vertical Major Axis and C(h,k):
From the standard equations as explained above, we can make the following observations:
- An ellipse is symmetric with respect to the major and minor axis. If (x, y) is a point on the ellipse, (-x, y), (x, -y) and (-x, -y) also exist on the ellipse.
- The foci are present on the major axis which can be deduced by finding the intercepts on the axes of symmetry. This means that the major axis is along the x-axis when the coefficient x2 has the bigger denominator. The major axis is along the y-axis when the coefficient of y2 has the bigger denominator.
Steps for writing the equation of the ellipse in standard form:
- Complete the square for both the x-terms and y-terms and move the constant to the other side of the equation
- Divide all terms by the constant
Example 1:
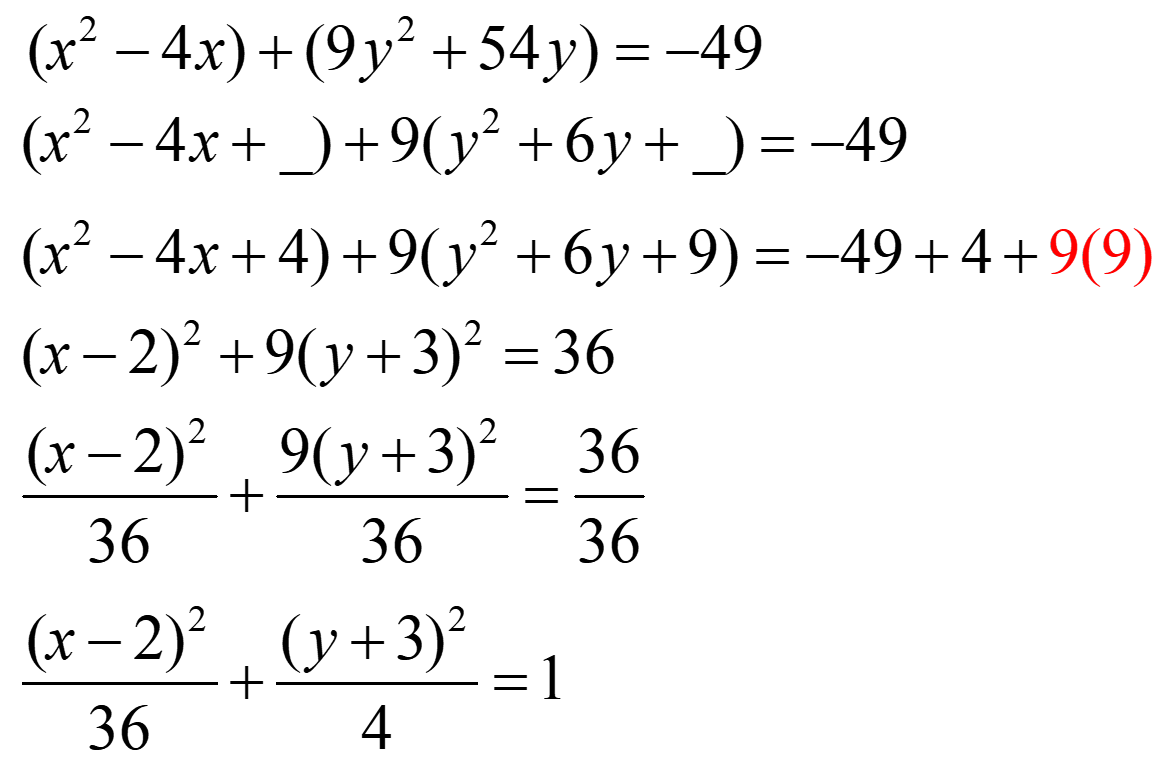
Steps for graphing the ellipse:
- Put equation in standard form
- Graph the centre (h, k)
- Graph the foci (look at the equation to determine your direction)
- Graph a units and –units from the centre to get the endpoints (horizontally if under x, vertically if under y)
- Connect the endpoints
Example 2: Write the following equation in standard form, then graph it:

Example 3: Find the equation of the ellipse with foci at (8,0) and (-8,0) and a vertex at (12,0).
- First, place these points on axes. The F and F’ are the foci.
- Since the vertex is on the horizontal axis, the ellipse will be of the form:
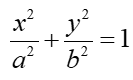
- The values of a and b need to be determined.
- Because the foci are at 8 and -8, c = 8. Also, the vertex is at (12,0), hence a = 12. Relating these values to the standard form for an ellipse whose centre is at the origin and whose major axis is horizontal, the equivalence c2 = a2 – b2 applies. Solve for b2 where
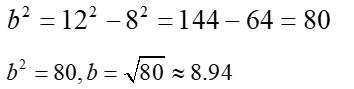
- The value of a is 12, and a2 is 144.
- So the equation of the ellipse is: