When the graph of a linear function passes through the points A (x1, y1) and B (x2, y2), then the equation can be written as:
$y-y_{1}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}(x-x_{1})$
It can also be written as:
$\frac{y-y_{1}}{y_{2}-y_{1}}=\frac{x-x_{1}}{x_{2}-x_{1}}$
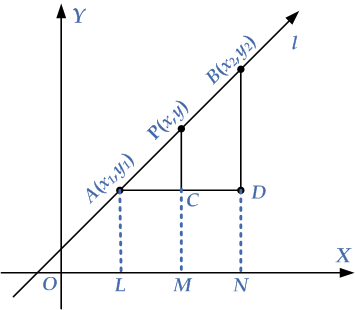
For verifying this equation let P(x,y) be any point on the given line that passes through A(x$_{1}$,y$_{1}$) and B(x$_{2}$,y$_{2}$), as shown in the graph above. From A and B, we draw AL and BN that is perpendicular to the X-axis. From point P, we draw PM that is also perpendicular to the X-axis. Also, from A draw a line that is perpendicular to AD on BN.
Consider the similar triangles ADB and ACP constructed on the graph above. By the definition of a slope and similar triangles we can deduce that:
$\frac{PC}{BD}=\frac{AC}{AD}$
Likewise,
PC = PM -CM = y- y1
BD=BN-DN = y2 – y1
AC=LM=OM-ON = x-x1
AD=LN=ON-OL=x2-x1
Substitute the point values: $\frac{PC}{BD}=\frac{AC}{AD}$
$\frac{y-y_{1}}{y_{2}-y_{1}}=\frac{x-x_{1}}{x_{2}-x_{1}}$
This equation can also be written as:
$y-y_{1}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}(x-x_{1})$
There is another way of deriving the two-point form of the equation of a line. Recall that the slope of the line AB is the ratio of the change in y to the change in x as shown in the equation below:
$m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$
$\Delta y=m\Delta x$
$y-y_{1}=m(x-x_{1})$
Substitute the equation for m:
$y-y_{1}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}(x-x_{1})$
The two- form is the starting step to derive the standard equation of a line when two points are given.
Example 1. Find a general form equation and point-slope form equation for the line through the pair of points (-1,2) and (5,/-4)?
Let ordered pair (x$_{1}$, y$_{1}$) be (1, 2) and (x$_{2}$, y$_{2}$) be (5, -4). Substitute these values in the two-point form equation
$y-y_{1}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}(x-x_{1})$
$y-2=\frac{-4-2}{5-1}(x-1)$
$y-2=-\frac{6}{4}(x-1)$
$4(y-2)=-6(x-1)$
$4y-8=-6x-6$
$4y+6x-8+6=0$
$4y+6x-2=0$
The point intercept form can be written from the two-point form as:
$y-2=\frac{-4-2}{5-1}(x-1)$
$y-2=-\frac{6}{4}(x-1)$
Make y as the subject of the equation
$y=\frac{-6x+6}{4}+2$
$y=\frac{-6x}{4}+\frac{6}{4}+2$
$y=\frac{-3}{2}x+\frac{6}{4}+2$
$y=\frac{-3}{2}x+\frac{7}{2}$
Here, m = -3/2 and b=7/2
Example 2. Write the two-point form and the general equation of the linear function y whose graph passes through the given pairs of points: (-1, 1) and (2, -4)
Plugging (x₁ , y₁) = (-1, 1) and (x₂, y₂) = (2, -4), we get:
$\frac{y-1}{-4-1}=\frac{x+1}{2+1}$
Simplify the equation to get the general equation:
$\frac{y-1}{-5}=\frac{x+1}{3}$
$3(y-1)=-5(x+1)$
$3y-3=-5x-5$
$5x+3y+2=0$
The two-point method to derive a general equation can not be used for the vertical line.
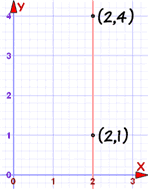
Step 1. Find the slope:
$m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$
$m=\frac{4-1}{2-2}=\frac{3}{0}=undefined$
We can convert the two-form equation as a function of x to obtain the general equation.
$y-y_{1}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}(x-x_{1})$
$y-y_{1}\frac{x_{2}-x_{1}}{ y_{2}-y_{1}}=x-x_{1}$
$y-1\frac{2-2}{4-1}=x-2$
$y-1\frac{0}{3}=x-2$
$o=x-2$
$x=2$