Mathematical reasoning is required to determine if a mathematical argument is correct or incorrect in order to construct mathematical arguments. There are two types of reasoning identified in mathematics: deductive and inductive.
Inductive reasoning requires processing from a series of specific cases to a general statement. The conclusion in an inductive argument is not guaranteed towards a specific conclusion.
For example: What is the next number in the sequence 6, 13, 20, 27,…There is more than one correct answer.
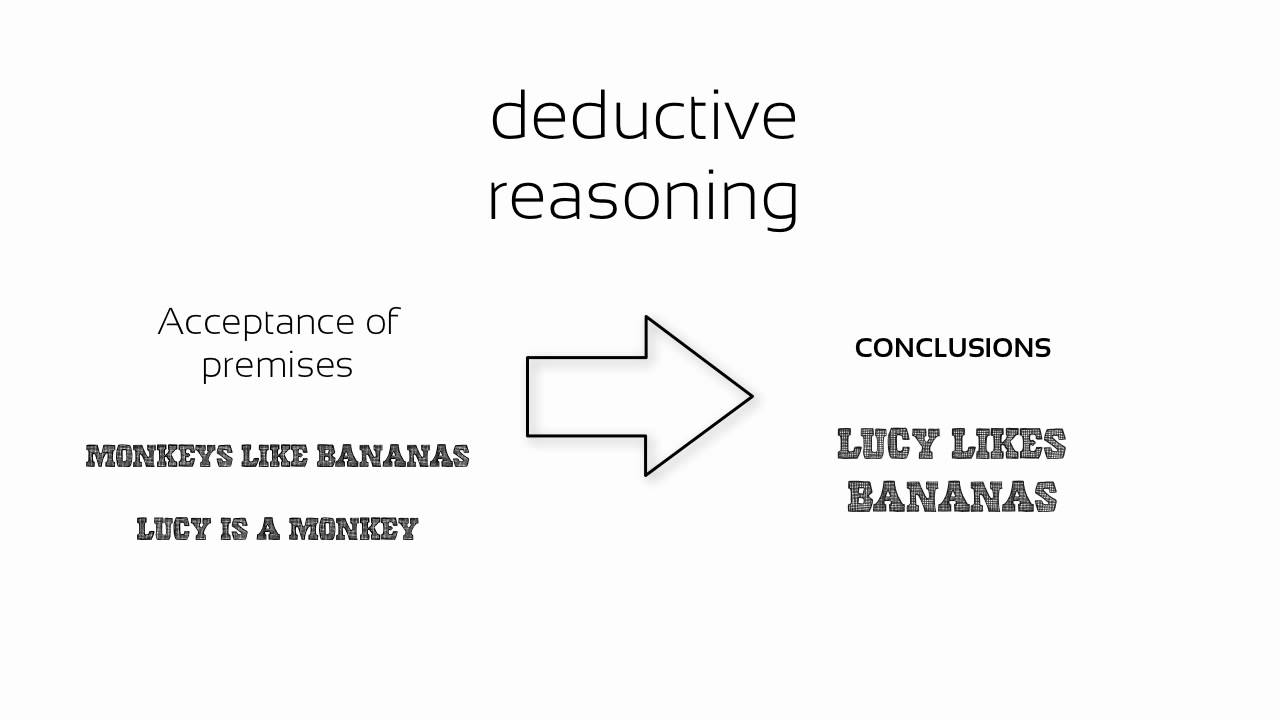
Deductive reasoning draws a logic pathway where one goes from a general statement to a specific instance. For any particular section of premises, if there is guaranteed outcome, the criticization are said to be valid. If the outcome is not that much guaranteed (at least 1 instance in which the conclusion does not follow), or it follows inductive reasoning then the argument is said to be invalid.
For example, All men are mortal. (major premise). Socrates is a man. (minor premise). Therefore, Socrates is mortal. (conclusion)
A mathematically acceptable statement is a sentence that is either true or false but not both. So ‘7 is an odd integer’ is a statement. But ‘π is a cool number’ is not a mathematical statement because it can be a cool number to some and boring to others.Note that ‘8 is an odd integer’ is also a statement, but it is a false statement.
Example: There are 50 days in a month.
The period mentioned in the above statement is variable, some months have 30, others have 31 while February may have 28 or 29 days. But the sentence above is always false because the maximum number of days in a moth can never exceed 31 days. Therefore, this sentence is a statement.
Example: How far is London from here?
This sentence contains a word here which is not conclusive. Therefore it is not a statement.
If p represents a statement, then the negation of p is denoted by ∼p and read as not p. The ~p signifies the denial of the statement.
Example: Everyone in England speaks English.
The negation of this statement is not everyone in England speaks English. It means that some or atleast one person in England does not speak English.
Example: Asia is a continent.
The negation of this statement is: It is false that Asia is a continent. It can also be written as Asia is not a continent.
A compound statement contains connecting words between two statements or more statements. Ex. There is something wrong with the tube light or the wiring.