Introduction to the Binomial Theorem
In the field of elementary algebra, the binomial expansion or the binomial theorem illustrates the expansion or the algebraic expansion of binomial’s powers.
As per the theorem, it’s likely to expand or extend (x + y)n polynomial in the direction towards the sum which involves terms in a .xb yc form, where b & c exponents are regarded as the non-negative integers, having b + c = n, plus ‘a’ coefficient of each of the terms is a particularly positive value integer which is dependent on the value n & b.
Let’s say (for n = 5),
(x+y)⁵ = x⁵ + 5x⁴y + 10x³y² + 10x²y³ + 5xy⁴ + y⁵
Now, in the term a. xb yc, ‘a’ coefficient is called the binomial coefficient. These binomial coefficients which contain changing b & n which can be arranged to create Pascal’s Triangle.
History
Talking about the history, binomial theorem’s special cases were revealed to the world since 4th century BC; the time when the Greek mathematician, Euclid specified binomial theorem’s special case for the exponent 2. There’s the proof that binomial theorem mentioned for the cubes was made known to the people in the 6th-century AD in India.
The binomial coefficients expressed in the context of the combinational quantities, signifying different methods of choosing k objects out of the ‘n’ objects without any replacement and these were the interest of the archaic Indian Mathematicians.
The first and original known reference to this combinational hassle is the “Chandaḥśāstra”, given by the known Indian lyricist, Pingala in 200 BC, which involves a particular method for its answer.
The reporter, Halayudha who belonged to the 10th century AD describes this way using which is now renowned to the people as Pascal’s triangle. With the arrival of the 6th century AD, the Indian mathematicians possibly familiar as to how to signify this in the quotient form as Binomial Theorem:
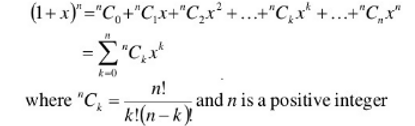
Note: there are n+1 terms here and also, a clear statement concerning this theorem, which was found in the 12th-century text Lilavati by another great Indian mathematician, Bhaskara.
Al-Karaji described the triangular pattern of the binomial coefficients and also provided a mathematical proof of both the binomial theorem and Pascal’s triangle, using an early form of mathematical induction.
For our knowledge, the very first formulation or the institution of the binomial theorem in addition to the binomial coefficients’ table, you can found in the knowledgeable work by Al-Karaji, which is quoted by Al-Samaw’al at the age of 19 in his mathematical treatise, “al-Bahir”, which means “the brilliant in algebra”.
Al-Karaji who was a Persian and had his main interest in the field of mathematics and engineering explained binomial coefficients’ triangular pattern and even used the mathematical proof of both Pascal’s triangle and the binomial theorem with the use of the initial mathematical induction’s form.
The binomial theorem has a great significance as the Persian mathematician and poet, Omar Khayyam was possibly having the well-known knowledge of higher-order formulas, even though many of the mathematical works of his are under wraps as they have been lost.
Small degrees’ binomial expansion were made familiar in the 13th century with Yang Hui’s mathematical works and also with the contribution given by Chu Shih-Chieh in the mathematics field.
Yang Hui featured a method in the early 11th-century text of Jia Xian, also known as Chia Hsein, even those writings are lost now.
In the year 1544, the German monk, mathematician, and a Protestant reformer introduced “binomial coefficient” term & showed us how to express and use (1 + a)ⁿ in terms of (1 + a)ⁿ-¹ through Pascal’s triangle.
Blaise Pascal who also invented the first digital calculator and he also studied the onymous triangle broadly in the year 1653.
Although, numbers’ pattern was known already to the Mathematician of Europe and of the late Renaissance which includes Niccolò Fontana, Stifel, Simon Stevin, and Tartaglia.
Usually, Isaac Newton was trusted with the generalized & conceptualized binomial theorem, authentic for any of the rational exponents.