Measuring angles in radians and in degrees and conversion of one into other
Radian Measure of an Angle
The measurement of an angle is resolved from the initial side by number of rotation towards the terminal side.
One method to measure the angles is in the form of radians. To define, what’s a radian, make use of circle’s central angle (an angle whose top or vertex is circle’s center).
A radian is the measurement of the central angle which intercepts an arc which is ‘s’ in the below figure and which is equal to radius’s length ‘r’ of the circle.
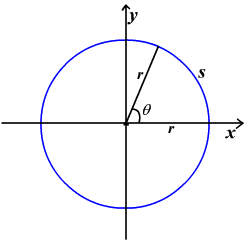
Taking into consideration the circle’s circumference which is 2πr, one revolution around the circle of ‘r’ radius correlates to 2π radians angle as s / r = 2πr / r = 2π radians.
Measuring Angles in Degree Form.
In one full rotation, there’s 360 degrees and by one full rotation, we mean one complete circle.
The Degree Symbol: °
For instance – 90° = 90 degrees
Measuring Degrees
Oftentimes we do measure degrees with the help of a protractor:
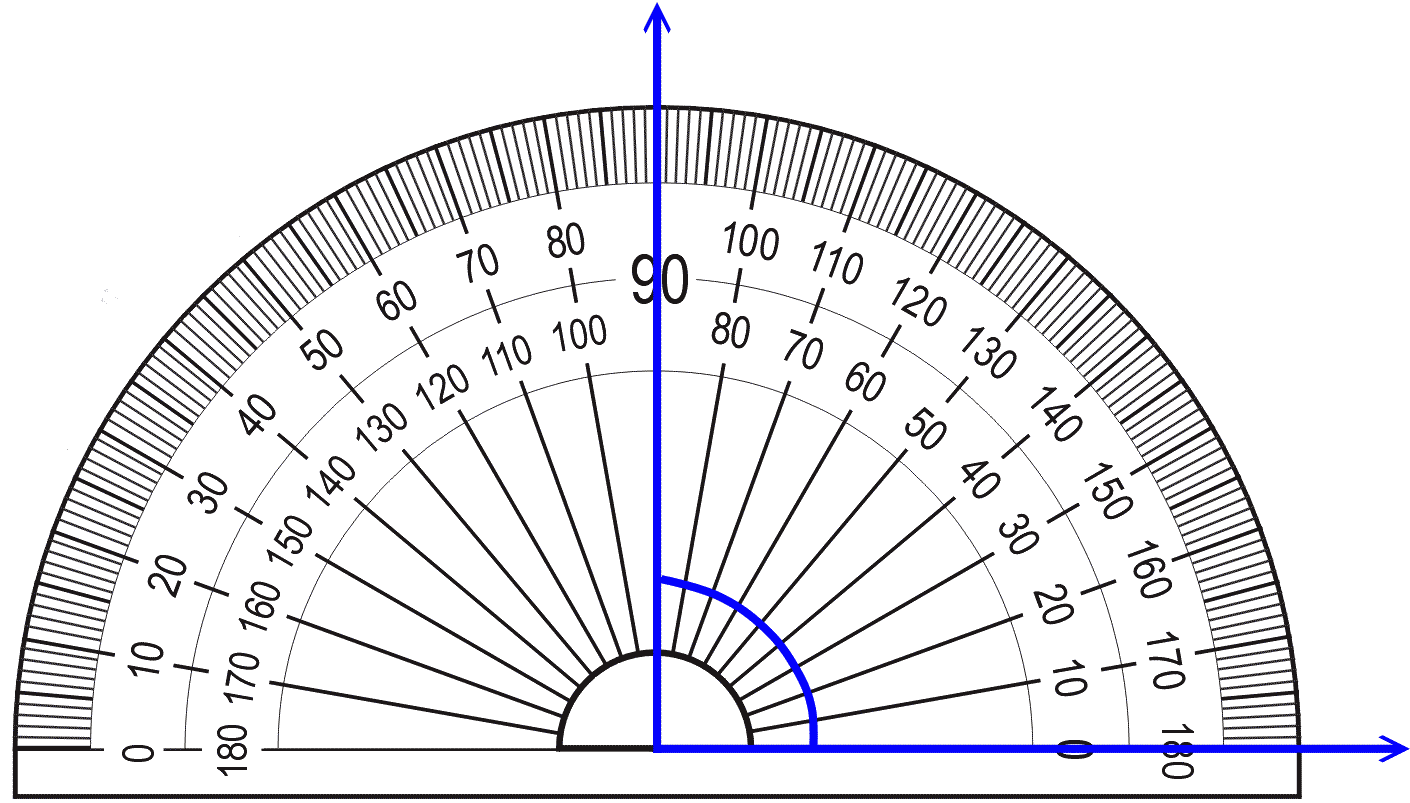
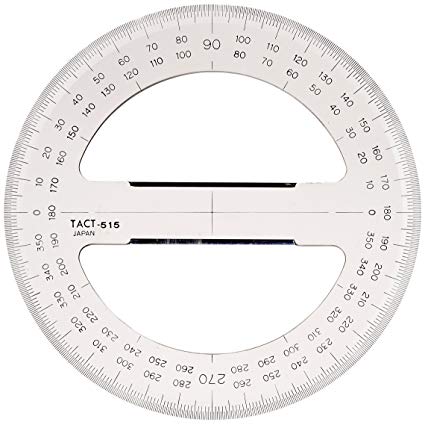
A radian is known as arc’s angle in the circle which is made by encircling circle’s radius surrounding its circumference. The representation of the angle is in between the two lines via degrees and radians.
Circle’s total angle is equal to 360 degrees or it can understood as 2 radians. With the benefit of conversion of radians to degrees, you can convert angles which are described in the form of radians into degree form.
Radians to Degrees Formula is given as,
Degrees= Radians × 180 / π
Solved Examples
Question: Convert 2.56° to radians ?
Answer:
Given below is the formula for converting radians into degree is,
Degrees = Radians∗180 / π
Degrees = 2.56∗180 / π
Degrees = 3,225.6 / π
Degrees = 146.75
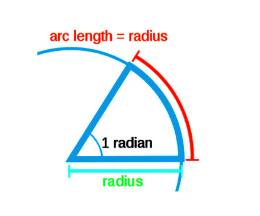
The radian refers to angular measure’s standard unit. The measurement of angle in radians which is mathematically equal to the length of the unit circle’s corresponding arc.
The connection or the relationship between radius and arc length of the circle illustrates circle’s radian.
The radian and degree formula are used for the conversion of radians into degrees or degree into the radian.
Radian into Degree Formula
Radian = Arc Length / Radius Length
Radian = Degree * π / 180
So, here a few angles and their relative radian measures
- 30 degrees = π / 60
- 60 degrees = π / 30
- 90 degrees = π / 2
- 120 degrees = 2π / 3
- 225 degrees = 5π / 4
- 240 degrees = 4π / 3
- 300 degrees = 5π / 3
- 360 degrees = 2π