Simple problems (that illustrate basic principles and understanding of the subject as well as real-life situations)
Optimization using calculus:
A box has a square base of side x cm and a height of h cm.It has a volume of 1 litre (1000 cm3)
For what value of x will the surface area of the box be minimised?[… and hence the cost of production be optimised]
Solution: To use calculus we must express the surface area in terms of x alone … so we must find h in terms of x.For a cuboid, volume = lbh … so in this case 1000 = x2h.
And so,
The box consists 6 rectangles, two of area x2 cm2 and four of area xhcm2
Total Surface Area, S = 2x2 + 4xh
S = 2x2 + 4000x–1
= 0 at stationary points
- 4x = 4000x–2
- x3 = 1000
- x = 10
![]()
If x< 10, 4x< 40 and 4000x–2> 40. SodS/dx< 0 … a decreasing function. If x> 10, 4x> 40 and 4000x–2< 40. SodS/dx> 0 … an increasing function. Minimum turning point is x = 10
If x = 10 then h = 10.
A cube of side 10 cm has a volume of 1000 cm3 and the smallest possible surface area.
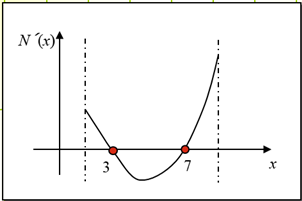
Example: During one study of red squirrelsthe number in one area was modelled by the function
N(x) = x3 – 15x2 + 63x – 10, 1 <x< 12
Where xdenotes the number of years since the study started.During what years was this a decreasing function
Solution: N(x) = x3 – 15x2 + 63x – 10, 1 <x< 12
- N´(x) = 3x2 – 30x + 63
N´(x) = 0 at stationary points
3x2 – 30x + 63 = 0 x = 3 or 7
The sketch illustrates that N´(x) < 0 for 3 <x< 7.
The population was decreasing from the 3rd and 7th years of the survey.
Example: A man of height 2 metres walks at a uniform speed of 6 km/h away from a lamp post which is 5 metres high. Find the rate of length of his shadow increasing with speed.
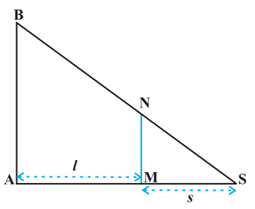
In the figure above, Let AB be the lamp-post, the lamp being at the position B and let MN be the man
at a fixed time t and let AM = l metres. Then,MS is the shadow of the man. Let MS = s metres. Recall that ∆MSN ≈∆ASB. Hence,
$\frac{MS}{AS}=\frac{MN}{AB}$
AS = 2.5s (as MN = 2 and AB = 5 (given))
l=AM = 2.5 s – s = 1.5s.
l = 1.5s
$\frac{dl}{dt}=1.5\frac{ds}{dt}$
Since $\frac{dl}{dt}=6 km/h$, the length of the shadow increases at the rate of 4 km/h