Need for complex numbers, especially √1, to be motivated by inability to solve some of the quadratic equations
Complex Numbers
The complex number is defined as the combination of the imaginary number and a real number.
Let’s say, a + bi
So here, a = real part, whereas b = imaginary part, and lastly, i = √-1
Either Part Can Be Zero
As mentioned above that complex numbers consist of two parts i.e. real and imaginary but either of these parts can be zero, therefore, all the imaginary and real numbers are called the Complex Numbers also.
| Complex Number | Real Part | Imaginary Part | |
| 3 + 2i | 3 | 2 | |
| 5 | 5 | 0 | Purely Real |
| −6i | 0 | −6 | Purely Imaginary |
A complex number can be represented as the point:
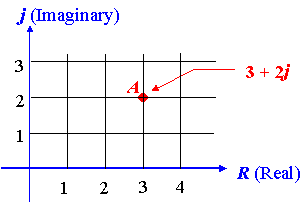
The complex number = 3 + 2i
Now, comes the Quadratic Equation
Quadratic Equation
The standard form of the Quadratic Equation is:
Where, a, b, c are the real numbers & also, a≠0.
Equation’s root is given by or the quadratic formula is given by:
x = −b + √(b2 − 4ac) / 2a
x = −b − √(b2 − 4ac) / 2a
Here, the discriminant is “D” = √b2 – 4ac
Equation’s two roots are ax² + bx + c = 0 are
X = -b ± √b2 − 4ac / 2a
Now, when solving the quadratic equation we get, three conditions occur and they are:
- When b2 − 4ac > 0; so, these 2 roots are distinct and real
- When b2 − 4ac = 0; then you’ll be getting one real root and a curve which just touches the x-axis.
- When b2 − 4ac < 0; In this very case, there exist no real solutions as there are no real squares present for giving -ve “b2 − 4ac”.
Therefore, from the below image’s graph view, the curve of y = ax2 + bx + c directly lies below or above the x-axis.

In recent times only, it’s relatively seen that the mathematics has been easy going with these respective roots when b2 − 4ac < 0. Its roots would be known as the imaginary ones as “1” at the time of the Renaissance. The quadratic also would be considered as the unsolvable.
If to visualize that √−1 exists, and it acts very much like alternate numbers, then accordingly the quadratic’s two roots ax² + bx + c = 0 can be expressed in x = A ± B √−1 form.
Where, A = -b / 2a & B = √ 4ac − b² / 2a; they are the real numbers. But the question arises that what these roots mean? So, till the beginning of the 19th century, later the numbers which were imaginary given so useful work particularly in the field of Gauss and Cauchy.
Notation : We’ll be going to write ‘i’ for the value √−1 – This is known as the standard notation among the mathematicians; although many of the books, specifically those which were written for the physicists & the engineers, use the value j instead.
Hence, the need for the complex numbers has a very important role to play in mathematics!