The determinant of a square matrix (up to 3 × 3 matrices), properties of determinants, minors, co-factors and applications of determinants in finding the area of a triangle
To compute the inverse of a matrix, the determinant is required. For each square matrix A, there is a unit scalar value known as the determinant of A, denoted by det A or |A|.If det(A)=0, the matrix is said to be singular.The determinant contains the same elements as the matrix which are enclosed between vertical bars instead of brackets in a scalar equation. If A = [A] is a single element (1×1), then the determinant is defined as the value of the element
Then |A| =det A= a11
If A is (n x n), its determinant may be defined in terms of the order (n-1) or less.
The determinant of A = $\lbrack \begin{matrix}
3 & -2 & \\
17 & 11 & \\
\end{matrix}
\rbrack $ is written as $\vert \begin{matrix}
3 & -2 & \\
17 & 11 & \\
\end{matrix}
\vert $. For second-order determinants we use the following formula:
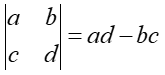
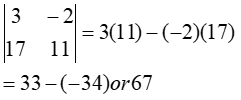
If A is an n x n matrix and one row and one column are deleted, the resulting matrix is an (n-1) x (n-1) submatrix of A.The determinant of such a submatrix is called a minor of A and is designated by mij, where i and j correspond to the deleted row and column, respectively. This means that mij is the minor of the element aij in A.
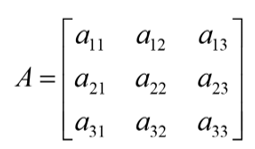
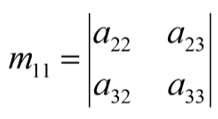

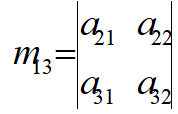
The cofactor Cij of an element aij is defined as:![]()
When the sum of a row number i and column j is even, cij = mij and when i+j is odd, cij =-mij
The determinant of an n x n matrix A can be written as:
The determinant of Ais essentially the sum of the products of the elements of the first row of A and their corresponding cofactors.
For using minors to calculate third-order determinants, each member of one row is multiplied by its minor. The signs of the product’s alternate, beginning with the second product. The definition below shows an expansion using the elements in the first for of the determinant. However, ANY row can be used.
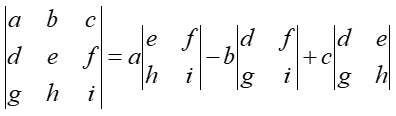
Example: Evaluate the determinant of A = $\lbrack \begin{matrix}
2 & 3 & 4 & \\
6 & 5 & 7 & \\
1 & 2 & 8 & \\
\end{matrix}
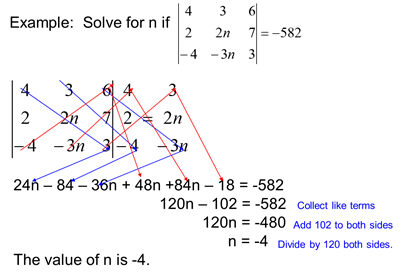
\rbrack $
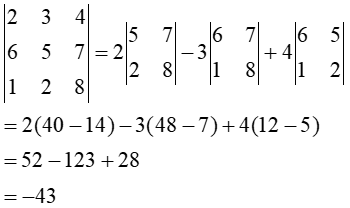
Example: Find the determinant
The cofactors of the first row are:
There is another simpler method utilizing diagonals for evaluating a third-order determinant.
- STEP 1: Write the first two columns on the right side of the determinant as shown below.
- STEP 2: Draw a diagonal from each element in the top row downwards and deduce the product of the numbers on each diagonal.
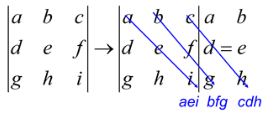
- STEP 3: Now draw a diagonal from each element in the bottom row upwards and deduce the product of the numbers on each.
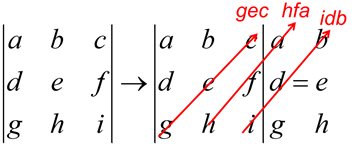
- To find the value of the determinant, add the products in the first set of diagonals, and then subtract the products from the second set of diagonals.
- The value is:aei + bfg + cdh – gec – hfa – idb
Determinants are utilized to calculate the area of a triangle when you know the coordinates of the three vertices. The area of a triangle whose vertices have coordinates (a, b), (c, d), (e, f) can be found by using the formula:
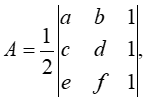
Example: Find the area of the triangle whose vertices have coordinates (-4, -1), (3, 2), (4, 6).
Assign values to a, b, c, d, e, and f in the above formula: a = -4, b = -1, c = 3, d = 2, e = 4, f = 6
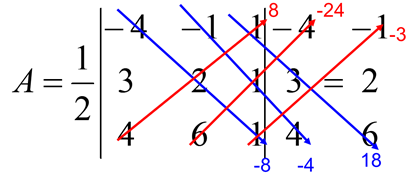
Now use the diagonal method and add the bottom products and subtract the top products: -8 + (-4) + 18 – 8 – (-24) –(-3) = 25. The value of the determinant is 25. And when we apply that to the area formula, we obtain ½ (25) = 12.5. The area of the triangle is 12.5 square units.
When one or more elements of a determinant are unknown, but the value of the determinant is known then we can use expansion to find the values of the variable.