The distance between point P= (x0, y0) and Line L: ax +by+c=0 is shown in the figure below.
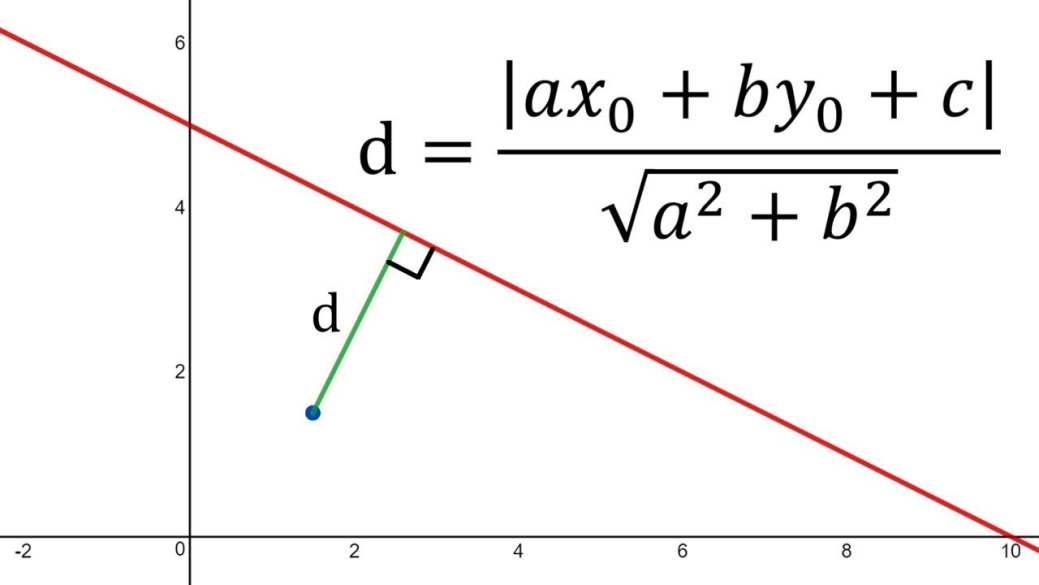
For the general equation
L= ax + by +c =0
m = -a/b
The shortest distance between a point, P and a line is a perpendicular line segment. The slope of the perpendicular line formed from the point. (Negative reciprocal from the given line)
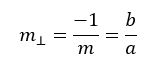
Now, to find the distance between point PP and line L,L, we can use a little geometry trick and have another line, parallel to L, that passes through P, let’s call it S. Likewise, we can have another line, this time parallel to T, that passes through the origin (0,0), let’s call it R.
since S passes through P and has the same slope as L, the equation of line S is:
$y-y_{0}=-\frac{a}{b}(x-x_{0})$
$y=\frac{-ax+ax_{0}+by_{0}}{b}$
The equation for line R is
$y=\frac{b}{a}x$
Since line S intersects line R:
$\frac{b}{a}x=\frac{-ax+ax_{0}+by_{0}}{b}$
Making x as the subject in the equation
$x=\frac{a(x_{0}+by_{0})}{a^{2}+b^{2}}$
Therefore, the intersection point between S and R can be written as:
$P_{1}(\frac{a(x_{0}+by_{0})}{a^{2}+b^{2}}, \frac{b(x_{0}+by_{0})}{a^{2}+b^{2}})$
Consider the point where Line L and R intersect. This happens at the
following line equations:
$y=\frac{b}{a}x=ax+by+c=0$
$y= -\frac{ax+c}{b}=\frac{b}{a}x=-\frac{bc}{a^{2}+b^{2}}$
Therefore, the intersection point between line L and R can be written
as:
$P_{2}(\frac{-ac}{a^{2}+b^{2}}, \frac{-bc}{a^{2}+b^{2}})$
For a line segment, the distance formula is as follows:
$d=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}$
For a line segment between P$_{1}$ and P$_{2}$ :

Example 1: Find the distance of the point (3, -5) from the line 3x -4y -26 = 0
In the above equation, using the general form of line equation, A=3, B=-4 and C=-26
Substitute these values in the distance equation:
$d=\frac{\vert Ax_{0}+By_{0}+C\vert }{\sqrt{a^{2}+b^{2}}}$
$d=\frac{\vert 3(3)-4(-5)-26\vert }{\sqrt{3^{2}+(-4)^{2}}}=\frac{\vert 9+20-26\vert }{\sqrt{9+16}}=\frac{\vert 3\vert }{\sqrt{25}}=\frac{\vert 3\vert }{5}=\frac{3}{5}$
The distance is 3/5 units.
Distance between Two Parallel Lines
Two lines are considered parallel to each other when the distance between them at any point is the same. In other words, if the slopes of both lines are the same, they will be parallel to each other. Consider two parallel lines l$_{1}$ and l$_{2}$ in XY-plane with equal slope = m.
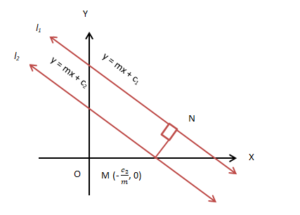
Y = mx + b$_{1}$
Y = mx +b$_{2}$
The distance between two parallel lines is deduced by the distance of a point from a line. The distance of this point is equal to the length of the perpendicular distance from any point to each line. Let N be the point through which the perpendicular to L$_{1}$ from point M (? c2/m, 0). From the previous derivation, we now that the distance between two lines is:
$d=\frac{\vert Ax_{0}+By_{0}+C\vert }{\sqrt{a^{2}+b^{2}}}$
Compare y = mx + b$_{1}$ and Ax + By + C = 0, in this case, A=m, B=1 and C = b$_{1 }$.Also x$_{1}$=-c$_{2}$/m and y$_{1}$=0
Therefore, substituting the values in equation for d:
$d=\frac{\vert m(-c_{2}/m)+1(0)+b_{1}\vert }{\sqrt{m^{2}+1^{2}}}=\frac{\vert -b_{2}+b_{1}\vert }{\sqrt{m^{2}+1}}$
Generalized equation :
$d=\frac{\vert b_{1}-b_{2}\vert }{\sqrt{A^{2}+B^{2}}}$